ဒြပ်ထု တည်မြဲမှု နိယာမ

မီသိန်း လောင်ကျွမ်းပေါက်ကွဲခြင်းတွင် အောက်စီဂျင် အက်တမ် ၄ လုံး၊ ဟိုက်ဒရိုဂျင် အက်တမ်လေးလုံး၊ ကာဘွန် အက်တမ် ၁ လုံးတို့သည် ဓာတ်ပြမှုမတိုင်မီနှင့် ပြီးနောက် ထိုအတိုင်း ဆက်လက်ရှိကြပြီး ဓာတ်ပြုမှုမတိုင်မီ ဒြပ်ထုစုစုပေါင်းသည် ဓာတ်ပြုမှုပြီးနောက် ဒြပ်ထုစုစုပေါင်းနှင့် တူညီသည်။

ရူပဗေဒနှင့် ဓာတုဗေဒတို့တွင် ဒြပ်ထု တည်မြဲမှု နိယာမ (အင်္ဂလိပ်: law of conservation of mass or principle of mass conservation) ဆိုသည်မှာ စွမ်းအင်နှင့် ဒြပ်ထု ကူးပြောင်းဖလှယ်ခြင်းများအတွက် အပိတ်စနစ် (သို့) ပြင်ပမှစွက်ဖက်မှုမရှိသောစနစ်၌ ဒြပ်ထုသည် အချိန်နှင့်အမျှ ကိန်းသေရှိသည်။ အကြောင်းမှာ ထိုစနစ်၏ ဒြပ်ထုသည် ပြောင်းလဲနိုင်စွမ်းမရှိပေ။ ထို့ကြောင့် ပမာဏကို ထပ်မံ ထည့်သွင်းရန်လည်း မဖြစ်နိုင်သကဲ့သို့ ဖယ်ရှားရန်လည်း မဖြစ်နိုင်ပေ။ အကျိုးဆက်အားဖြင့် ဒြပ်ထုပမာဏကို အချိန်နှင့်အမျှ တစ်ညီတည်း(ကိန်းသေအဖြစ်) ထိန်းသိမ်းထားသည်။

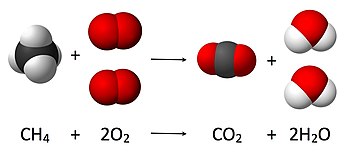
နိယာမက ဒြပ်ထုသည် ဖန်တီး၍လည်းမရ၊ ဖျက်ဆီး၍လည်းမရဟု သွယ်ဝိုက်ညွှန်းဆိုသည်။ သို့ရာ၌ အကာသတွင် ဒြပ်ထုကို ပြောင်းလဲစီစဉ်နိုင်သည် (သို့) ပါဝင်ဒြပ်ထုသားများသည် ပုံသဏ္ဌာန်ပြောင်းလဲသွားနိုင်သည်။ ဥပမာအနေဖြင့် ဓာတုဓာတ်ပြုခြင်းများ၌ ဓာတ်ပြုမှုမတိုင်မီ ဓာတုပါဝင်ပစ္စည်းများ၏ ဒြပ်ထုသည် ဓာတ်ပြုမှုပြီးနောက် ပါဝင်ပစ္စည်းများ၏ ဒြပ်ထုနှင့် ညီမျှလေသည်။ ထို့အတွက်ကြောင့် အပိတ်စနစ်တွင် ဓာတုဓာတ်ပြုခြင်းနှင့် စွမ်းအင်နိမ့် သာမိုဒိုင်းနမစ်ဖြစ်စဉ်များအတွင်း ဓာတ်စမ်းပစ္စည်းများ၏ စုစုပေါင်း ဒြပ်ထုသည် ရလဒ်/ထွက်ပေါ်လာသော ပစ္စည်းများ၏ စုစုပေါင်း ဒြပ်ထုနှင့် တူညီပေသည်။

ဒြပ်ထုတည်မြဲခြင်း အယူအဆကို ဓာတုဗေဒ၊ မက္ကင်းနစ်၊ ငွေ့ရည် ဒိုင်းနမစ် စသည့် နယ်ပယ်များစွာ၌ ကျယ်ပြန့်စွာ အသုံးပြုကြသည်။ သမိုင်းကြောင်းအရ ဒြပ်ထုတည်မြဲခြင်းကို မီခေးလ်း လောမန်နော့ဆော့ဖ် (Mikhail Lomonosov) က ဓာတုဓာတ်ပြုမှုများဖြင့် တသီးတခြား သရုပ်ပြသခဲ့ပြီး အန်ထွမ်း(န်) လာဗွေ့ဇီယေ (Antoine Lavoisier) က နောက်ပိုင်းတွင် ပြန်လည်ရှာဖွေတွေ့ရှိခဲ့သည်။ ဤနိယာမဖော်ထုတ်ခြင်းသည် အဂ္ဂိရတ်ပညာမှသည် ခေတ်ပေါ် သိပ္ပံဘာသာရပ်ဖြစ်သည့် ဓာတုဗေဒဘာသာရပ်တို့၏ တိုးတက်လာမှု၌ လွန်စွာအရေးပါခဲ့၏ ။

ဒြပ်ထုတည်မြဲခြင်းနိယာမသည် ခန့်မှန်ခြေအားဖြင့် အပြောင်းအလဲမရှိခဲ့ပဲ ဆက်လက်တည်ရှိနေကာ ဂန္ထဝင်ရူပဗေဒ ဘာသာရပ်မှ ပေါက်ဖွားလာသော ယူဆချက်များ၏ တစ်စိတ်တစ်ပိုင်းဖြစ်သည်ဟု ယူဆကြသည်။ ဤနိယာမကို ဒြပ်ထု-စွမ်းအင် ညီမျှမှုနိယာမ (mass-energy equivalence) အောက်၌ ကွမ်တမ်မက္ကင်းနစ်၊ အထူးနှိုင်းရသီအိုရီတို့နှင့် ကိုက်ညီစေရန် ပြုပြင်မွမ်းမံရန် လိုအပ်လျက်ရှိသည်။ ဒြပ်ထု-စွမ်းအင် ညီမျှမှုနိယာမက စွမ်းအင်နှင့် ဒြပ်ထုတို့သည် စုစုပေါင်းကိန်းသေပမာဏကိုဖွဲ့စည်းသည်ဟု ဆိုထားသည်။ လွန်စွာတက်ကြွတုံ့ပြန်တတ်သော စနစ်များအတွက် ဒြပ်ထုတစ်မျိုးတည်း တည်မြဲခြင်းသဘောသည် ကိုက်ညီမှုမရှိကြောင်းပြသရာ အကြောင်းမှာ အမှုန် ရူပဗေဒတွင် အမှုန်-ဆန့်ကျင်အမှုန်တို့၏ ဒြပ်မှ စွမ်းအင်ပြောင်းလဲခြင်းဖြစ်စဉ်နှင့် နျူကလီးယားဓာတ်ပြုတုံ့ပြန်ခြင်းတို့တွင် မကိုက်ညီ၍ဖြစ်သည်။

ဒြပ်ထုသည် အပွင့်စနစ်များတွင် စုစုပေါင်းကိန်းသေတန်ဖိုး၌ ထိန်းသိမ်းထား၍ ပုံမှန်အားဖြင့် မရပေ။ ဆိုလိုသည်မှာ အပွင့်စနစ်ဖြစ်သောကြောင့် ဝင်လာသော၊ ထွက်သွားသော ဒြပ်ထုအမျိုးမျိုး၊ စွမ်းအင်ပုံစံအမျိုးမျိုးတို့ကို ခွင့်ပြုထားသောကြောင့်ဖြစ်၏ ။ သို့ရာတွင် နျူကလီးယားဓာတ်ပြုခြင်း (သို့) ရေဒီယိုဓာတ်သတ္တုကြွခြင်းများ ပါဝင်ပတ်သက်မှုမရှိလျှင် အပူ၊ စက်ပိုင်းဆိုင်ရာအလုပ်၊ လျှပ်စစ်သံလိုက်ဖြာထွက်ခြင်း ကဲ့သို့သောစနစ်များ၌ ထွက်သွားသော (ဝင်လာသော) စွမ်းအင်ပမာဏသည် ထိုစနစ်၏ ဒြပ်ထုတွင် တက်/ကျခြင်းအဖြစ် မတိုင်းတာနိုင်လောက်အောင် အများအားဖြင့် သေးငယ်ကြသည်။

ကြီးမားသောဆွဲအားပါဝင်ပတ်သက်သော စနစ်များတွင်ကား ယေဘုယျနှိုင်းရသီအိုရီကို ထည့်သွင်းစဉ်းစားရမည်ဖြစ်ပြီး ထို၌ ဒြပ်ထု-စွမ်းအင် တည်မြဲခြင်း နိယာမသည် ပိုမိုကျယ်ပြန့် ရှုပ်ထွေး၍ အနက်ဖွင့်ဆိုမှုများစွာ ရှိကြသည်။ အထူးနှိုင်းရသီအိုရီမှာကဲ့သို့ ဒြပ်ထု၊ စွမ်းအင် နှစ်မျိုးစလုံးကို တိတိကျကျ၊ ရိုးရိုးရှင်းရှင်း ကိန်းသေတန်ဖိုး၌ ထိန်းသိမ်းထားနိုင်မှုမရှိချေ။