စာရင်းအင်း ပညာ

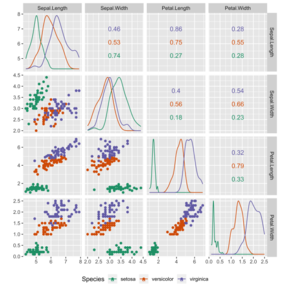
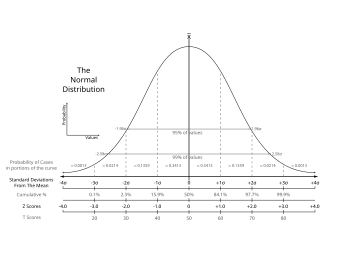
စာရင်းအင်း ပညာ သို့မဟုတ် စာရင်းအင်းသင်္ချာ (statistics) သည် သင်္ချာဘာသာ၏ ဘာသာကွဲတစ်ရပ်ဖြစ်ပြီး အဓိကအားဖြင့် အချက်အလက်များ (data) ကို စုဆောင်းခြင်း (collection)၊ ခွဲခြမ်းစိတ်ဖြာ ဆန်းစစ်ခြင်း (analysis)၊ အဓိပ္ပာယ်ဖော်ထုတ်ခြင်း (explanation) နှင် ရှင်းလင်း တင်ပြခြင်း (presentation) စသည့် ဖြစ်စဉ်များ ပါဝင်သည်။[၁][၂][၃] ယင်းပညာရပ်ကို သဘာဝ နှင့် လူမှုရေး သိပ္ပံ မှသည် အစိုးရ နှင့် စီးပွားရေးလုပ်ငန်းများအထိ နယ်ပယ်များစွာတွင် ကျယ်ပြန့်စွာ အသုံးပြုနိုင်သည်။ သိပ္ပံပညာဆိုင်ရာ သို့မဟုတ် စက်မှုလုပ်ငန်းဆိုင်ရာ သို့မဟုတ် လူမှုရေးဆိုင်ရာ ပြဿနာများ ဖြေရှင်းရန်အတွက် စာရင်းအင်းသင်္ချာကို အသုံးချရာတွင် စိတ်ဝင်စားသော လူ့အဖွဲ့အစည်းတစ်ခု သို့မဟုတ် လေ့လာကောက်ချက်ဆွဲမည့် အုပ်စုကြီးတစ်ခု ဆုံးဖြတ်သတ်မှတ်ခြင်းဖြစ်စေ၊ ရှေးမှကောက်ယူရရှိထားသော စာရင်းအင်းအချက်အလက်ကို အခြေခံယူ၍ ပြုလုပ်ထားသောပုံစံ (statistical model) ကို အသုံးပြုကာ နောက်ဖြစ်နိုင်ခြေကို လေ့လာကောက်ချက်ဆွဲခြင်းဖြစ်စေ ဤသို့စတင်တွေးတောခြင်းမှာ ပုံမှန်လုပ်ရိုးလုပ်စဉ် ဖြစ်သည်။ စာရင်းအင်းဆိုင်ရာ လူ့အဖွဲ့အစည်းတစ်ခု သို့မဟုတ် အုပ်စုကြီးတစ်ခု (population) ဆိုသည်မှာ "လူမျိုးပေါင်းစုံ" (သို့) "တိုင်းပြည်တွင်နေထိုင်သောလူအားလုံး" (သို့) "ပုံဆောင်ခဲ (cyrstal) တစ်ခုတွင် ပါဝင်သော အက်တမ် (atom) အားလုံး" စသည်တို့ဖြစ်သည်။ စာရင်းအင်းတွက်ချက်ရန် လုံလောက်သော နမူနာကျပန်းကောက်ခြင်း၊ စစ်တမ်းကောက် (surveys) ယူမည်လော၊ ကိုယ်တိုင်စမ်းသပ်မှု (experiments) လုပ်ကာ အချက်အလက်ထုတ်လုပ်မည်လား အစရှိသည့် အချက်အလက်မည်သို့ စုဆောင်းမည်ဟု စီစဉ်ခြင်း မှစ၍ အချက်အလက် (data)များကို ရှုထောင့်အမျိုးမျိုးမှ ကိုင်တွယ်အသုံးပြု အဖြေရှာခြင်းများသည် စာရင်းအင်းသင်္ချာနယ်ပယ်အောက်တွင် ရှိသည်။[၄]
ယခုအခါ စာရင်းစုပညာသည် ခေတ်စားလျက်ရှိသည်။ ပမာ အားဖြင့် လူဦးရေ တိုးတက် ဆုတ်ယုတ်မှုကို သိရှိနိုင်ရန် သန်းခေါင်စာရင်းကောက်ခြင်း၊ တိုင်းပြည်လူထု တစ်မျိုးသားလုံး ၏ တစ်နှစ်အတွက် ဝင်ငွေသုံးငွေ စာရင်းများ၊ မြန်မာနိုင်ငံ လယ်များမှ ပျမ်းမျှတစ်ဧက စပါးအထွက်နှုန်းသိနိုင်ရန် စာရင်း များ စုဆောင်းခြင်း အစရှိသည့် စံနစ်များသည် စာရင်းစုပညာ နှင့် သက်ဆိုင်သည်။
စာရင်းစုပညာ ဟူသည်မှာ အဓိကအားဖြင့် တိုင်းထွာ ရေ တွက်၍ ရကောင်းသော အရာဝတ္ထုများ၏ အတိုင်းအထွာ ပမာဏများကို စာရင်းပြုလုပ်၍ ယင်းဝတ္ထုပစ္စည်းတို့နှင့် ဆက် စပ်သော ကိစ္စတို့ကို လေ့လာခြင်း ဖြစ်သည်။ ပမာဆိုသော် ဖွားသေ စာရင်းများ စုဆောင်းခြင်းဖြင့် တိုင်းပြည်လူထု၏ ပျမ်းမျှ သက်တမ်းကို ခန့်မှန်းနိုင်၏။ ထိုစာရင်းများကို အသုံး ပြု၍ အသက်အာမခံလုပ်ငန်းကို အောင်မြင်စွာ ဆောင်ရွက် နိုင်၏။ ဒေသအလိုက် နေ့စဉ် မိုးရွာသော စာရင်းများ ပြုစု ခြင်းဖြင့် ဒေသတစ်ခု၌ နှစ်စဉ် မိုးနည်းသည် များသည်ကို သိနိုင်၏။ ရာသီဥတုကို ကြိုတင် ခန့်မှန်းနိုင်၏။ ထိုနည်း အတူ စပါးအရောင်းအဝယ် ဈေးနှုန်းစာရင်းများ၊ အဝတ်အထည် ဈေးနှုန်းစာရင်းများ၊ သားငါးပုဇွန် အစားအစာများ၏ ဈေးနှုန်း စာရင်းများ စုဆောင်းလေ့လာခြင်းဖြင့် လူထု သက်သာချောင်ချိ မှု တိုးတက်ခြင်း၊ ဆုတ်ယုတ်ခြင်းတို့ကို သိနိုင်၏။ မြို့တစ်မြို့ ၏ လူသေစာရင်းတွင် သက်ဆိုင်သော ရောဂါ အမျိုးအမည်ကို လေ့လာခြင်းဖြင့် မည်သည့်ရောဂါအတွက် ဆေးဝါးနှင့် ဆရာ ဝန်များ အထူးလိုအပ်ကြောင်း သိနိုင်၏။
အသုံးပြုလေ့ရှိသော နည်းတစ်ခုမှာ စံနမူနာနည်းဖြစ်သည်။ ပမာအားဖြင့် မအူပင်ခရိုင်တွင် စပါးတစ်ဧက မည်မျှ ထွက် သည်ကို သိလိုသည်ဟု ဆိုကြပါစို့။ ခရိုင်တစ်ခုလုံးထွက်သော စပါးစာရင်းများ၊ စိုက်ပျိုးသော ဧကအားလုံး၏ စာရင်းများကို စုဆောင်းရပေလိမ့်မည်။ သို့ရာတွင် ဤမျှ ကျယ်ပြန့်များပြား သော စာရင်းများကို အတိအကျ ရယူစုဆောင်းရန် မလွယ်ကူ ပေ။ အချိန်များစွာ ကုန်မည်။ လူများစွာ ကူညီဆောင်ရွက်ရ ပေမည်။ ထိုကြောင့် ဖြတ်လမ်းနည်း အလွယ်နည်းမှာ မအူပင် ခရိုင်အတွင်းရှိ သင့်တော်သော လယ်ကွက်ဆယ်ခုကို ရွေးချယ် ၍ စပါးထွက်ကို အသေးစိတ် စုံစမ်းခြင်း ဖြစ်၏။ ထိုဆယ် ကွက်ကို ရွေးချယ်ရာ၌ သင့်တော်မည်ထင်သော လယ်ကွက် ဆယ်ကွက်ကို ရွေးချယ်ခြင်း သို့မဟုတ် လယ်ကွက် ၁ဝဝ၊ ၂ဝဝ အထဲမှ မဲနှိုက်၍ရသော လယ် ၁ဝ ကွက်ကို ရွေးချယ် ခြင်း ဟူ၍လည်း နည်းအမျိုးမျိုး ရှိ၏။ သင့်တော်သလို အခြေ အနေအရ ဆောင်ရွက်ရမည် ဖြစ်သည်။ဤနည်းအားဖြင့် အချိန် အနည်းငယ်အတွင်း စရိတ်များစွာ မကုန်ဘဲ မအူပင်ခရိုင်၏ တစ်ဧက ပျမ်းမျှစပါးထွက်နှုန်းကို သိနိုင်၏။ ခန့်မှန်းနိုင်၏။ ထိုကြောင့် စီးပွားရေးအကြောင်းအရာများ၊ အုပ်ချုပ်မှုကိစ္စများ၊ စက်ရုံကြီးများ၌ ကုန်ထုတ်စရိတ်၊ တစ်နာရီတွင် ကုန်ချော ပစ္စည်း အထွက်နှုန်း စသည်များကို သိရှိနိုင်ရန် ဤနည်းကို အသုံးပြုကြ၏။ ရက်တိုလတို စုံစမ်းရေးအဖွဲ့များကလည်း ဤစံနစ်ကို အသုံးပြုကြ၏။
စာရင်းစုပညာတွင် ဇယားများနှင့် ဇယားကွက်ပုံစံ အမျိုး မျိုးကို အသုံးပြုရသည်။ ပမာအားဖြင့် အနှစ် ၅ဝ အတွင်း မြန်မာနိုင်ငံ စပါးဈေး အတက်အကျ အခြေအနေများ၊ လူဦးရေ တိုးတက်မှုများကို ဇယားများဖြင့် ရေးဆွဲဖော်ပြခြင်းသည် တိုးတက်မှု ဆုတ်ယုတ်မှုများကို ရှင်းလင်းစွာ နားလည်နိုင် စေသည်။
စာရင်းစုပညာဖြင့် အမှန်ကို အတိအကျ မသိနိုင်။ သန်း ခေါင်စာရင်း၊ တိုင်းပြည် စပါးထွက်စာရင်း၊ မိုးရွာစာရင်းများ သည် နယ်အသီးသီးမှ ကောက်ခံရသော စာရင်းများဖြစ်၍ မှားယွင်းချက် အနည်းငယ်ရှိနိုင်သည်။ သို့ရာတွင် ထိုစာရင်း များသည် များစွာ တန်ဖိုးရှိ၏။ ထိုစာရင်းများဖြင့် အနှစ် ၅ဝ အတွင်း လူဦးရေ တဖြည်းဖြည်း တိုးပွားလာခြင်း၊ မြန်မာနိုင်ငံ စပါးထွက် တစ်နှစ်ထက်တစ်နှစ် တိုးတက် ဆုတ်ယုတ်ခြင်းများ၊ ရန်ကုန်မြို့တွင် ပြည်မြို့ထက် နှစ်စဉ် မိုးနှစ်ဆရွာသွန်းခြင်း စသည်များကို သိနိုင်၏။
သတိပြုရမည့်အချက်မှာ စာရင်းများ စုဆောင်းရာ၌ စံနစ် တကျ ဖြစ်စေအပ်သော အချက်ပင်တည်း။ မှန်ကန်နိုင်သမျှ မှန်ကန်စွာ ဂဏန်းများ၊ စာရင်းများကို ကောက်ယူနိုင်လေလေ၊ ထိုစာရင်းများ၌ တန်ဖိုးရှိလေလေ ဖြစ်သည်။ စာရင်းစု ပညာကို တိုင်းပြည်အသီးသီးတို့က တစ်နေ့တစ်ခြား ပိုမို လေ့လာဂရုပြု ကြောင်း တွေ့ရှိရ၏။ စီးပွားရေး၊ ဘဏ္ဍာရေး၊ စိုက်ပျိုးရေး၊ လူမှုရေးအဖြာဖြာနှင့် သက်ဆိုင်သော သုတေသီပုဂ္ဂိုလ်တို့ အတွက် များစွာ တန်ဖိုးရှိသော ပညာရပ်တစ်ခု ဖြစ်သည်။ [၅]
နိဒါန်း
[ပြင်ဆင်ရန်]စာရင်းအင်းပညာသည် ယခုအခါ ပညာရပ်နယ်ပယ်အသီးသီးတွင် အသုံးပြုလျက်ရှိသည်။ပညာရေး၊ ဆေးပညာ၊ အင်ဂျင်နီယာ၊ ကွန်ပျူတာ စသည့်နယ်ပယ်များအပြင် အထူးသဖြင့် လူမှုရေးသုတေသန နှင့် စီးပွားရေးသုတေသန တို့တွင် အလွန် အသုံးဝင်သော ဘာသာရပ်တစ်ခုဖြစ်သည်။ လူမှုရေး နှင့် စီးပွားရေးပြဿနာအချို့ကို စာရင်းအင်းပညာဖြင့် လေ့လာ ဖြေရှင်းနိုင်သည်ကို တွေ့ရသည်။ ခေတ်မီသော သုတေသနတွေ့ရှိချက်များကို လေ့လာလိုလျှင်သော်လည်းကောင်း၊ တင်ပြချက်များရေးသားပြုစုရာတွင်လည်းကောင်း၊ သုတေသနလုပ်ငန်းများလုပ်ကိုင်ရာတွင် လည်းကောင်း၊ စာရင်းအင်းပညာရပ်ဆိုင်ရာ ဘာသာစကားကို အထိုက်အလျောက်နားလည် သဘောပေါက်ထားပြီး ဖြစ်ရန် အရေးကြီးသည်။ စာရင်းအင်းပညာရပ်သည် ပညာရပ်နယ်ပယ်အများစုတွင် သိပ္ပံနည်းကျ လေ့လာရာ၌ အသုံးကျသည့် ဘာသာရပ်တစ်ရပ်ဖြစ်သည်။ စာရင်းအင်းပညာသည် မည်သည့်နေရာတွင်မဆို ကြိုတင်ခန့်မှန်းသည့်နေရာတွင် အဓိက အသုံးပြုကြသည်။
သမိုင်းကြောင်း
[ပြင်ဆင်ရန်]စာရင်းအင်းပညာ၏ မူရင်း အင်္ဂလိပ်စကားလုံးမှာ statistics ဖြစ်သည်။(မြန်မာလို စာရင်းအင်းပညာဆိုသော စကားလုံးကို မည်သူစတင်သည်ဟု မသိရှိပါ။) ထို statistics ဆိုသော စကားလုံးသည် အီတလီစကား `ဖော်ပြသည်` ကိုတိုက်ရိုက်သုံးစွဲထားခြင်းဖြစ်သည်။[၆] စာရင်းအင်းပညာ၏အစသည် ၁၇ ရာစု အလယ်မှစတင်သည်ဟု ယူဆကြသည်။ လန်ဒန်မြို့မှ သာမန်စာအုပ်ဆိုင်ပိုင်ရှင်တစ်ဦးဖြစ်သော ဂျွန်ဂရန့် သည် ဘုရားကျောင်းများမှ ထုတ်ပြန်သော အပါတ်စဉ်သေစာရင်း များကို စုစည်းကာ ယခု သရုပ်ဖော်စာရင်းအင်းဟု ခေါ်ဆိုသော နည်းဖြင့် စာအုပ်(Natural and Political Observations Made upon the Bills of Mortality.)ထုတ်ဝေခဲ့သည်။ များမကြာမီတွင်ပင် ဂျွန်ဂရန့်သည် တော်ဝင်အဖွဲ့အစည်း၏ အဖွဲ့ဝင်အဖြစ် ရွေးချယ်ခြင်းခံခဲ့ရသည်။ ထိုအချိန်မှစတင်၍ စာရင်းအင်းပညာသည် လူဦးရေဆိုင်ရာ အသိပညာ၊ လူမှုရေးသိပ္ပံမှ အတွေးအခေါ်များ ကိုစတင် သက်ဝင်လာခဲ့သည်။ လူတို့၏အပြုအမူများကို လေ့လာရာတွင် အသုံးပြုသည့်အတွက် စာရင်းအင်းပညာကို သဘာဝတ္ထသိပ္ပံ ၏တိကျမှုတိုင်းတာရာတွင် အသုံးမပြုသင့်ဆိုသော အယူအဆများလည်း ပေါ်ထွက်ခဲ့သည်။ အသစ်အသစ်သော ကွဲပြားသည့်နယ်ပယ်အစုံမှ စာရင်းအင်းပညာကို သုံးစွဲလာကြသော်လည်း စာရင်းအင်းပညာရပ်ဆိုင်ရာဘာသာစကားတို့သည် လူအများနှင့် ဝေဝါးဆဲပဲဖြစ်သည်။ ၂ဝရာစုအတွင်းတွင် စာရင်းအင်းပညာရပ်ဆိုင်ရာ တိုးတက်မှုများစွာ ရှိလာသကဲ့သို့ အသုံးပြုသော ပညာရပ်နယ်ပယ်များလည်း များစွာ ပေါ်ထွန်းလာခဲ့သည်။ နက္ခတ္တဗေဒ၊ ရူပဗေဒ၊ ပထဝီနှင့် မြေမျက်နှာသွင်ပြင် စသည့် သိမ်မွေ့သော နယ်ပယ်များအထိ အသုံးချလာကြသည်ကို တွေ့ရသည်။
အဓိပ္ပာယ်ဖွင့်ဆိုချက်
[ပြင်ဆင်ရန်]စာရင်းအင်းပညာရပ်သည် အချက်အလက်များကို ကောက်ယူခြင်း၊ စုစည်းခြင်း၊ အကျဉ်းချုံ့ခြင်း၊ တင်ပြခြင်းနှင့် စိစစ်ခြင်းပြုလုပ်ရန် အသုံးပြုသော သိပ္ပံနည်းကျသည့် နည်းလမ်းတစ်ခုဖြစ်သည်။[၇]
အဆင့်များ
[ပြင်ဆင်ရန်]စာရင်းအင်းပညာရပ်ကို အသုံးပြု၍ သိပ္ပံနည်းကျလေ့လာရာတွင် အောက်ပါ အချက်များအတိုင်း အဆင့်ဆင့် ဆောင်ရွက်ရန်လိုသည်။ (က) အချက်အလက်များစုဆောင်းခြင်း (Collection of data) (ခ) အုပ်စုအလိုက်စုစည်းခြင်း (သို့မဟုတ်) မျိုးတူစုပြုခြင်း (Classification of data) (ဂ) အချက်အလက်များကို ပေါ်လွင်အောင် သရုပ်ဖော်ခြင်း (Description of data) (ဃ) တွေ့ရှိချက်များအပေါ်အခြေပြု၍ အဓိပ္ပာယ်ကောက်ခြင်းနှင့် ကောက်ချက်ချခြင်း (Interpretation and generalization of the results) တို့ဖြစ်သည်။
စာရင်းအင်းသင်္ချာ နည်းစနစ်များ
[ပြင်ဆင်ရန်]သရုပ်ဖော် စာရင်းအင်းသင်္ချာ
[ပြင်ဆင်ရန်]သရုပ်ဖော် စာရင်းအင်းသင်္ချာ သို့မဟုတ် ဖော်ပြစာရင်းအင်းပညာ (Descriptive Statistics)သည် လေ့လာမှုတစ်ခုတွင် နမူနာကျပန်းကောက်ခြင်း (sampling)မှ ရရှိသော အချက်အလက်များနှင့် ၎င်းတို့အပေါ် တိုင်းတာပုံများ (measures)၏ အခြေခံအင်္ဂါရပ်များကို အကျဉ်းချုပ် ဖော်ပြရန် အသုံးပြုသည်။ ထို့နောက် အဆိုပါ အင်္ဂါရပ်များကို ဆက်စပ်ပုံဇယားများအနေဖြင့် ဖော်ပြ၍ အရေအတွက်ဆိုင်ရာ ခွဲခြမ်းစိတ်ဖြာမှု (quantitative analysis)ပြုလုပ်ရာတွင် အသုံးပြုလေ့ရှိသည်။ အချုပ်အားဖြင့် ဤနည်းစနစ်ကို သုံး၍ ရှုပ်ထွေးများပြားသော အချက်အလက်များမှ အကျဉ်းချုပ်ကိုထုတ်ယူကာ နားလည်နိုင်ရန် ကြိုးစားလေ့ရှိသည်။[၈]
ဥပမာအားဖြင့်၊ ဘတ်စကက်ဘော ကစားသမားတစ်ယောက်၏ ဂိုးသွင်းရာခိုင်နှုန်းသည် ၎င်းကစားသမား၏ စွမ်းဆောင်ရည်ကို အကျဉ်းချုပ်ပြသော သရုပ်ဖော် စာရင်းအင်းသင်္ချာဆိုင်ရာ အင်္ဂါရပ်တစ်ခုဖြစ်သည်။ အကယ်၍ သူ၏ ဂိုးသွင်းရာခိုင်နှုန်းသည် ၃၃% ဟုဆိုလျှင်၊ သူ သုံးကြိမ်သွင်းလျှင် တစ်ကြိမ်ဝင်နိုင်သည်ဟု ယေဘုယျအားဖြင့် မှတ်ယူနိုင်သည်။[၈]
ကောက်ချက်ဆွဲ စာရင်းအင်းသင်္ချာ
[ပြင်ဆင်ရန်]ကောက်ချက်ဆွဲ စာရင်းအင်းသင်္ချာ သို့မဟုတ် ညွှန်ပြစာရင်းအင်းပညာ (Inferential Statistics) တွင်မူ လက်ရှိကောက်ယူထားသော နမူနာကျပန်းအုပ်စု (sample) အချက်အလက်များ၏ အင်္ဂါရပ်များမှတစ်ဆင့် အချက်အလက် ခွဲခြမ်းစိတ်ဖြာမှု (data analysis) ကို အသုံးပြု၍ အုပ်စုကြီးတစ်ခုလုံး (population) ၏ ဖြစ်နိုင်ချေ ပျံ့နှံ့မှုပုံစံ (probability distribution)ကို ကောက်ချက်ဆွဲယူရန် ကြိုးစားလေ့ရှိသည်။[၉]
ရည်ညွှန်းကိုးကား
[ပြင်ဆင်ရန်]- ↑ Oxford Reference။
- ↑ Romijn၊ Jan-Willem (2014)။ "Philosophy of statistics"။ Stanford Encyclopedia of Philosophy။
- ↑ Cambridge Dictionary။
- ↑ Dodge, Y. (2006) The Oxford Dictionary of Statistical Terms, Oxford University Press. ISBN 0-19-920613-9
- ↑ မြန်မာ့စွယ်စုံကျမ်း၊ အတွဲ(၃)
- ↑ Origin of the statistics and probability။ 2019-12-30 တွင် မူရင်းအား မော်ကွန်းတင်ပြီး။ 2020-09-26 တွင် ပြန်စစ်ပြီး။
- ↑ ပညာရေးသုတေသနပြုလုပ်နည်း၊ မြန်မာနိုင်ငံ ဝိဇ္ဇာနှင့်သိပ္ပံပညာရှင်အဖွဲ့၊ ပထမအကြိမ်၊ တက္ကသိုလ်များပုံနှိပ်တိုက်၊ ၂၀၀၁၊ ဇူလိုင်လ၊ ရန်ကုန်။ နှာ ၁၃၈။
- ↑ ၈.၀ ၈.၁ Trochim၊ William M. K. (2006)။ Descriptive statistics။ Research Methods Knowledge Base။ 14 March 2011 တွင် ပြန်စစ်ပြီး။
- ↑ Upton, G., Cook, I. (2008) Oxford Dictionary of Statistics, OUP. ISBN 978-0-19-954145-4.
